考点汇总

第一章

~~保密学的基本概念？~~
~~明文空间，密文空间，密钥空间的概念？~~
移位，数乘，仿射，维吉尼亚算法？
- okk
密码可能受到不同水平的攻击（四种）？

第二章（流密码）

流密码和分组密码区别？
- 内部有无记忆原件
- 对比特进行加密还是对分组进行加密
特征多项式、密钥流迭代函数、线性反馈移位寄存器的结构图互推？
- 特征多项式：$p(x) = x^4 + x + 1$
- 密钥流迭代函数：$a_k = a_{k-1} \bigoplus a_{k-4} \ k \ge 4$
- 线性反馈移位寄存器结构图
分析某个线性反馈移位寄存器是否能生成小m序列，周期，游程分布，是否满足golomb？
- okk
在已知线性反馈移位寄存器和加法加密变换的情况下，由明文和密文求得密钥？
- $m = 11110101,c = 10010001$
- $k_1…k_8 = 01100100$
- \[\begin{align} k_5 &= c_1k_4 + c_2k_3 + c_3k_2 + c_4k_1 \\ k_6 &= c_1k_5 + c_2k_4 + c_3k_3 + c_4k_2 \\ k_7 &= c_1k_6 + c_2k_5 + c_3k_4 + c_4k_3 \\ k_8 &= c_1k_7 + c_2k_6 + c_3k_5 + c_4k_4 \end{align}\]
- 解得
  
  $c_1 = 0, c_2 = 0, c_3 = 0, c_4 = 1$
golomb对伪随机周期序列提出的3个随机性公设?
- 在序列的一个周期内，0与1的个数相差至多为1
- 在序列的一个周期内，长为$i$的游程个数占游程有 $2^{n-i-1}$ 个，0，1游程各占一半，长为n-1的0游程有一个，长为n的游程有一个
- 异自相关函数（见书本）是一个常数
  - 周期为 $2^n - 1$ 的 $m$ 序列，这个常数就是 $-\frac{1}{2^n - 1}$

第三章（分组密码）

分组密码设置的两个基本准则（混淆，扩散）？
- 混淆：密文和密钥之间的依赖关系尽可能的复杂化，以防通过统计分析法进行破译
- 扩散：将明文的统计特性散布到密文中去，使得密文中的每一位由明文中的多位产生
分组密码如何工作？
- 分组密码的原理是乘积密码，即混淆和扩散两种基本密码操作的组合变换
- 具体实现上，选择较为简单的密码变换，在密钥控制下以迭代的方式进行加密变换，实现混淆和扩散
说明 SPN 网络？
- SPN网络是由多重S变换和P变换组合成的变换网络
- S变换是代换，起到混淆作用
- P变换是置换，起到扩散的作用
解释 SPN 的雪崩效应？
- 输入即使发生很小的变化，也会导致输出有很大的变化
DES流程？
- 算法描述
  - 明文分组和密文分组均为64比特，有效密钥56比特
  - 由初始置换， 16轮迭代，左右交换，逆初始置换组成
  - 加解密算法相同，只是解密子密钥和加密子密钥的使用顺序相反
- 具体细节（考试计算）
  - 初始置换，逆初始置换：对照置换表即可
  - 轮结构：将轮输入分为左右两部分
    - \[\begin{align} L_i = R_{i-1} \\ R_i = L_{i-1}\bigoplus F(R_{i-1}, K_i) \end{align}\]
  - 加密函数F：分别经过下面步骤
    - 扩展置换：32比特部分首先经过扩展置换得到48比特
    - 与子密钥异或：将48比特与子密钥异或
    - 压缩代换：8个S盒构成，每个S盒都是6比特输入，4比特输出
    - P置换
  - 子密钥生成
    - 64比特种子密钥取出8比特用于奇偶校验，剩余56比特
    - 56比特分为左右两部分，分别进行循环左移
    - 最后经过置换选择选出48比特得到子密钥
- 互补性
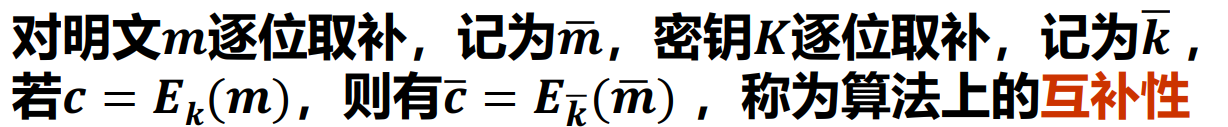
  - 由于算法中两次异或运算，使得 DES 在选择明文攻击下所需的工作量减半
多重 DES？
- 二重 DES?
  - $C = E_{K_2}[E_{K_1}[P]]$
  - $P = D_{K_1}[D_{K_2}[C]]$
- 两个密钥的三重 DES？
  - $C = E_{K_1}[D_{K_2}[E_{K_1}[P]]]$
  - $P = D_{K_1}[E_{K_2}[D_{K_1}[C]]]$
- 三个密钥的三重 DES？
  - $C = E_{K_3}[D_{K_2}[E_{K_1}[P]]]$
  - $P = D_{K_3}[E_{K_2}[D_{K_1}[C]]]$
有限域上的运算？
- 加法运算：异或
- 乘法运算：$mod\ \ x^8+x^4+x^3+x+1$
- x 运算
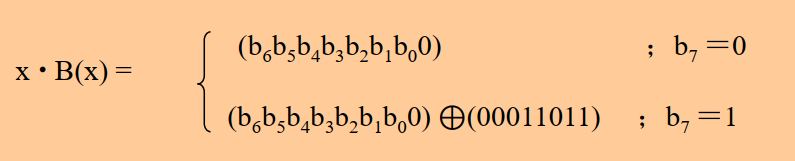
AES流程？
- 算法描述
  - 明文按字节分组得到明文矩阵，构建状态矩阵
  - 由初始置换， 9轮迭代，1轮最终轮组成
  - 加解密过程不相同，需要使用相应变换的逆变换，并且各个变换的使用顺序也不一样
- 具体细节
  - 轮函数：由以下四个部分组成
    - 字节代换：通过一个 S盒完成，即直接查表
    - 行移位：行循环左移，每一行左移单位不同
    - 列混合：每一个列多项式乘以一个固定多项式 $c(x) = 03x^3 + 01x^2 + 01x + 02$
    - 轮密钥加：异或
  - ~~子密钥生成~~
- 加解密流程
  - 加密和解密算法的计算网络相同，只是将各个部件换成对应的逆部件
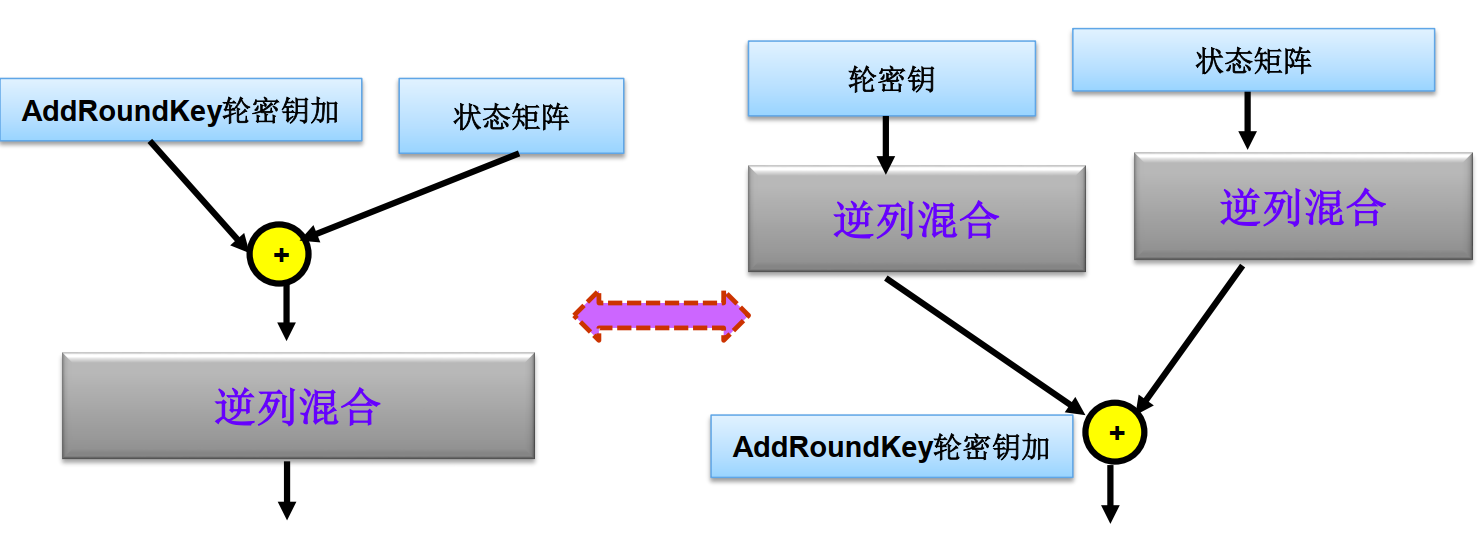
  - 但存在其他等价的解密流程
    - 交换逆字节代换和逆行移位不影响
    - 交换逆列混合和轮密钥加有影响，但是存在等价变形
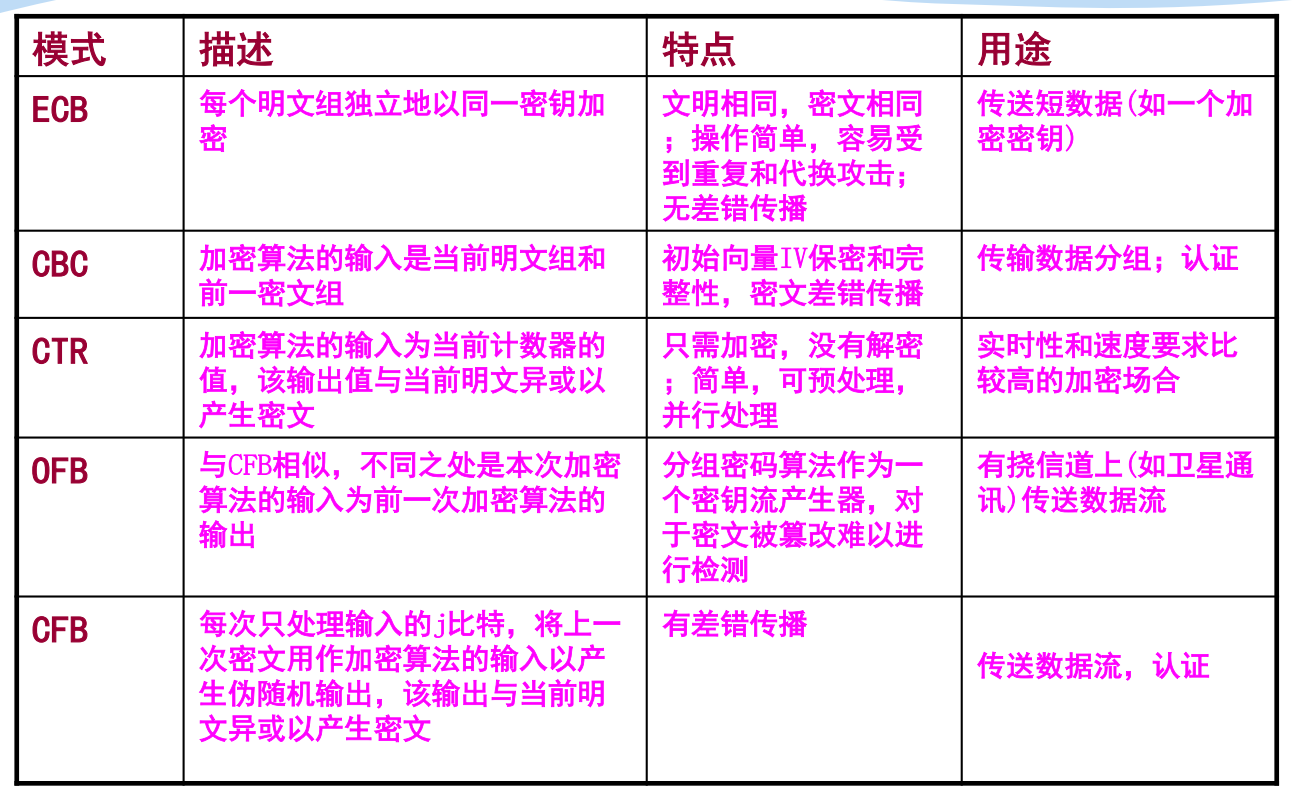
四种分组密码工作模式的优缺点，错误传播，加密解密流程？
- 电码本模式(ECB)
  - 加密解密流程
  - 特点
    - 直接用分组密码算法来进行消息的加密和解密
    - 可以并行计算
    - 相同明文得到相同密文（易于暴露明文的固有格式和统计特性）
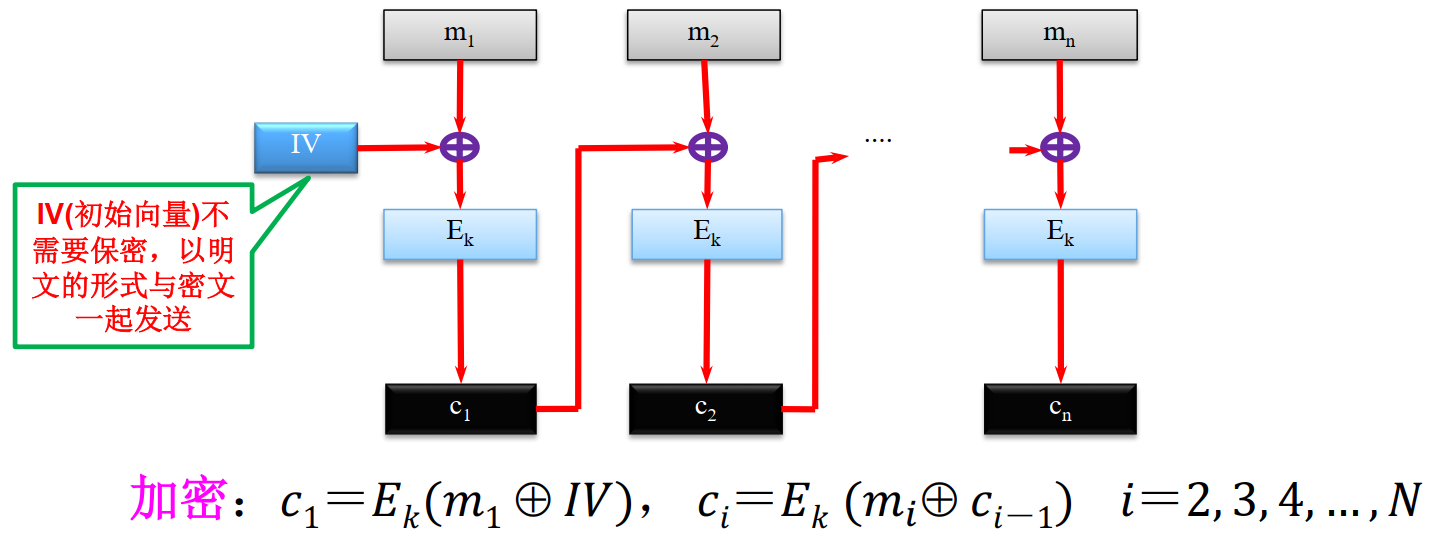
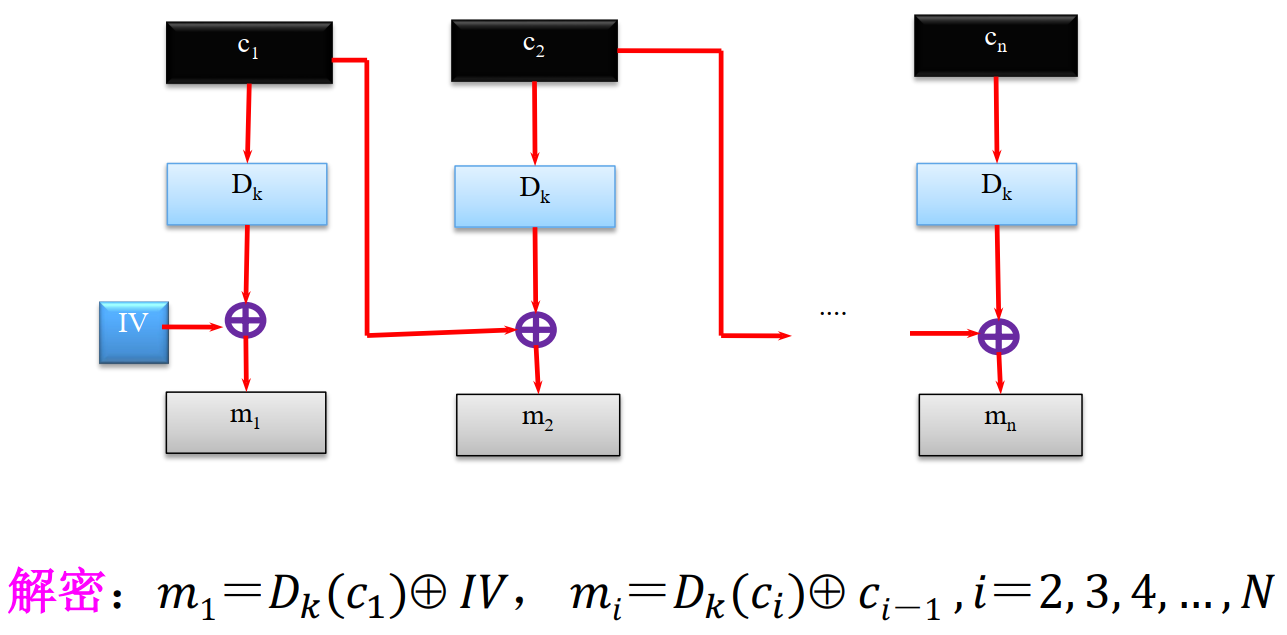
- 密码分组链接模式(CBC)
  - 加密解密流程
  - 特点
    - 加密输入是当前明文分组和前一密文分组的异或，形成一条链
    - 不能并行计算，相同明文得到不同密文
    - 传播错误
      - 明文有一分组有错，会使以后的密文组都受影响，但是解密时，除了该明文分组，其他明文分组不受影响
      - 传送过程中某组密文组出错时，则该组恢复的明文和下一组恢复数据出错（后面的解密明文组不受影响）
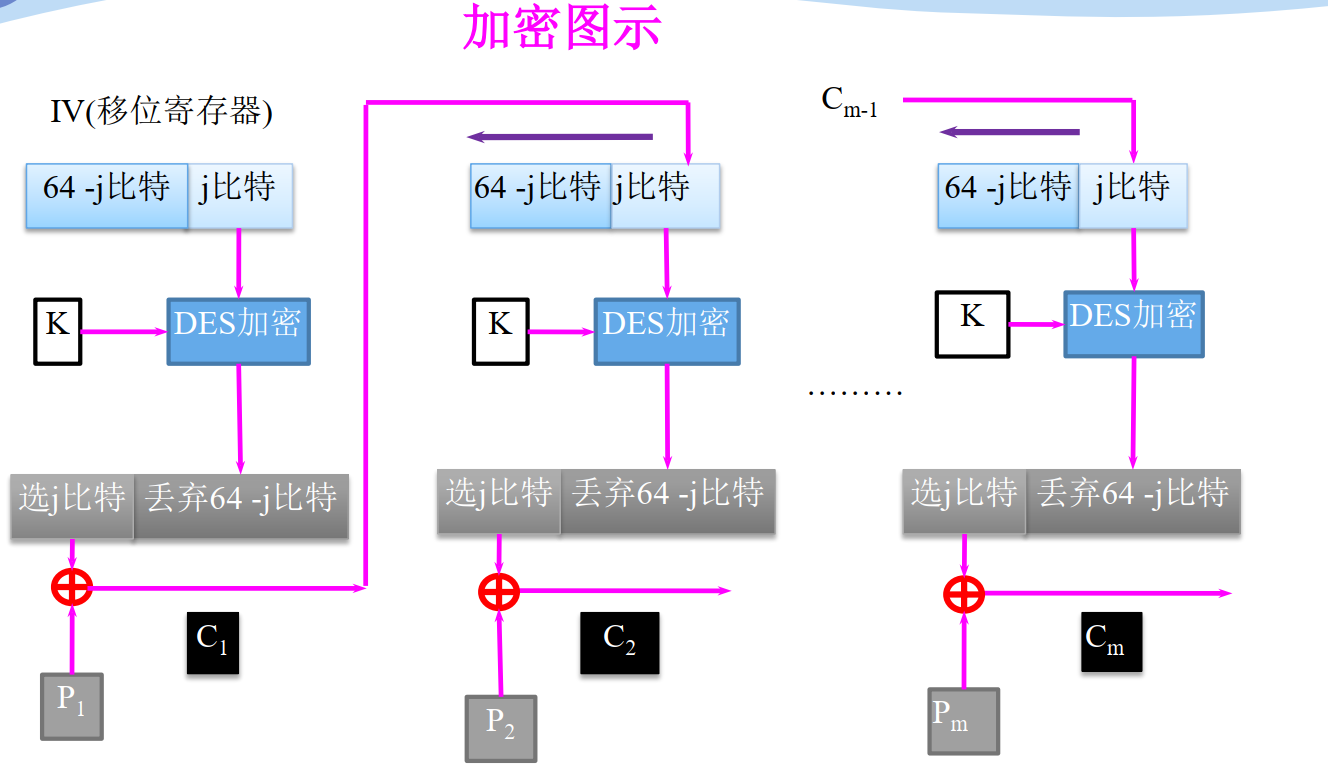
- 密码反馈模式(CFB)
  - 加密解密流程
  - 特点
    - 将加密算法作为一个密钥流产生器
    - 只使用加密算法
    - 自同步能力强，可以处理任意长度的消息
    - 传播错误
      - 明文某一组中有错，使以后的密文组都受影响，但经解密后，除原有误的一组外，其后各组都正确地恢复
      - 密文里的一位错误会引起明文的一个单独错误，此错误进入移位寄存器，导致密文成为无用信息，直到该错误从移位寄存器中移出
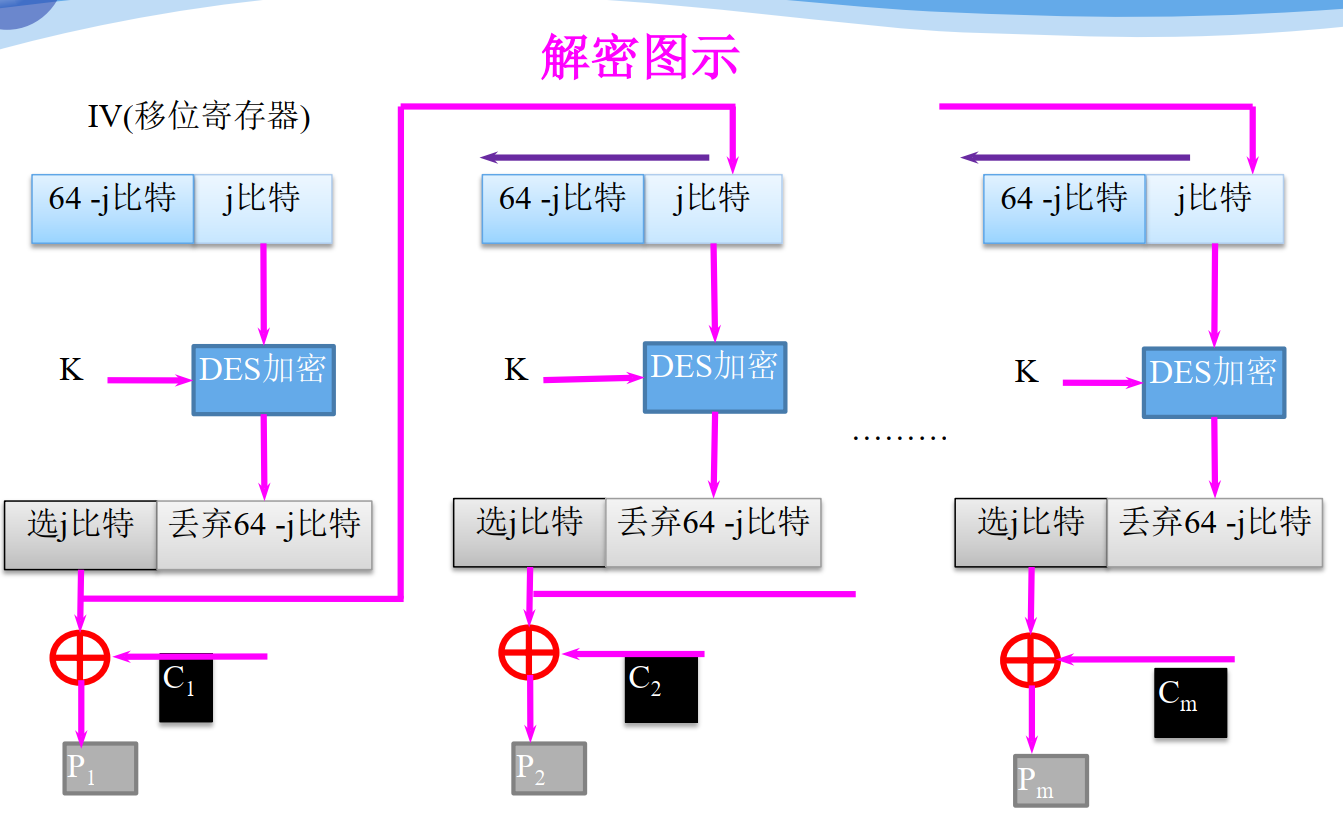
- 输出反馈模式(OFB)
  - 加密解密流程
  - 特点
    - 将加密算法作为一个密钥流产生器
    - 只使用加密算法
    - 错误不会传播
    - 难以检测篡改攻击
- 计数器模式(CTR)
  - 加密解密过程
  - 特点
    - 随机访问特性，对某一密文分组的处理与其它密文无关
    - 并行计算
    - 可以处理任意长度的数据，而且加解密过程仅涉及加密运算

第四章（hash函数）

hash函数概念？
- 本质是杂凑函数
- 任意长度的比特串x压缩为固定长度的比特串y
- 具有两个性质
  - 单向性：已知x，易求 y = H(x)；已知y=H(x) 求x困难
  - 无碰撞性：找(x1， x2)， x1≠x2， H(x1)= H(x2)，很困难
- 多数hash函数的设计都是迭代型的
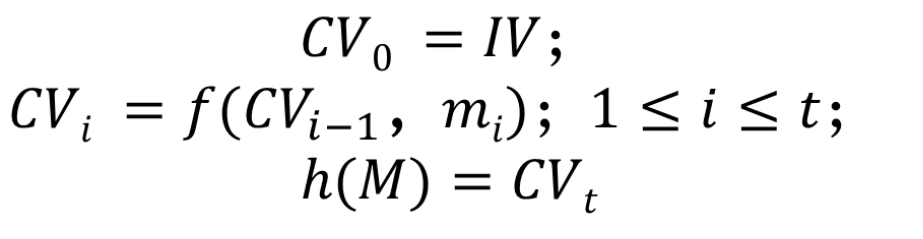
~~MD5哈希算法流程？~~
- 填充消息：填充后的消息长度为512的某一倍数减64，这一步是一定会发生的，填充比特是1-512比特之间，第一位为1，其余为0
- 补足长度：小端存储，$2^{64}$ 取模
- MD缓冲区初始化：小端存储
- 分组处理
  - $CV_0 = IV
    CV_{q+1} = CV_q \bigoplus RF_I[P_q, RF_H[P_q, RF_G[P_q, RF_F[P_q, CV_q]]]]
    MD = CV_L$
MD5和SHA-1的第一步（消息填充）？

第五章（公钥加密）

几个经典算法依赖的数学困难问题？
- 大整数因子分解问题(如公钥密码体制RSA)
  
  将两个大素数相乘容易，但对其乘积进行因式分解极其困难
- 有限域上的离散对数问题(如公钥密码体制ElGamal)
- 椭圆曲线上的离散对数问题(如公钥密码体制ECC)
- 背包问题（背包算法）
- 基于身份的密码体制（IBE）
椭圆曲线上的加法运算
- $y^2 = x^3 + ax + b,\ 4a^3+27b^2\neq0$
RSA算法（基于大整数因子分解）描述？
EIgamal算法描述？
快速指数算法？
ECC算法描述?
混合加密？

第六章（数字签名）

着重理解以下这一幅图（考得很模糊）？
什么样的公钥密码算法能够作为数字签名？
- 由公钥密码函数进一步修改得到：即加密算法和解密算法在调用的先后顺序发生改变后，结果不变
- $E(D(X)) = D(E(X)) = X$
基于RSA数字签名？
- 算法描述
- 为什么对消息的Hash函数值签名而不是直接对消息签名？
  - 加快签名速度：如果对整个消息签名（特别是对消息长度非常长），签名和验证过程会非常慢；使用Hash值签名，签名的速度都只与Hash值的长度有关
  - Hash函数可以两种抵御攻击：利用已有签名伪造新的消息，利用已有签名获得明文
基于EIGamal数字签名?
- 相同消息得到的签名值不同（秘密随机数 k的作用）
- Example

基于Schnorr数字签名?

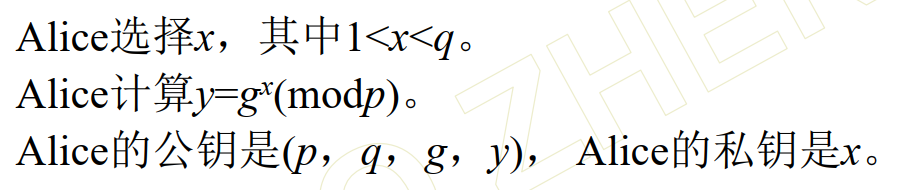
特性	EIGamal	Schnorr	说明
安全性	g为域GF(p)的本原元素	g只是域GF(p)的阶为q的元素，非本原元素	EIGamal离散对数阶高于Schnorr的，前者安全性更高
计算速度	r的长度为\|p\|， s的长度为\|p-1\|	e的长度为\|q\|， s的长度为\|q\|	除此之外，在Schnorr’中，$r=g^k(modp)$可以预先计算，后者的计算速度快

Shamir基于数字身份的数字签名？
- 算法描述
盲签名
- 签名者不知道即将发布的消息内容M，即消息不重要，重要的是签名

第七章（密码协议）

Diffie-Hellman密钥交换？
- 算法流程
- 举例
- 问题
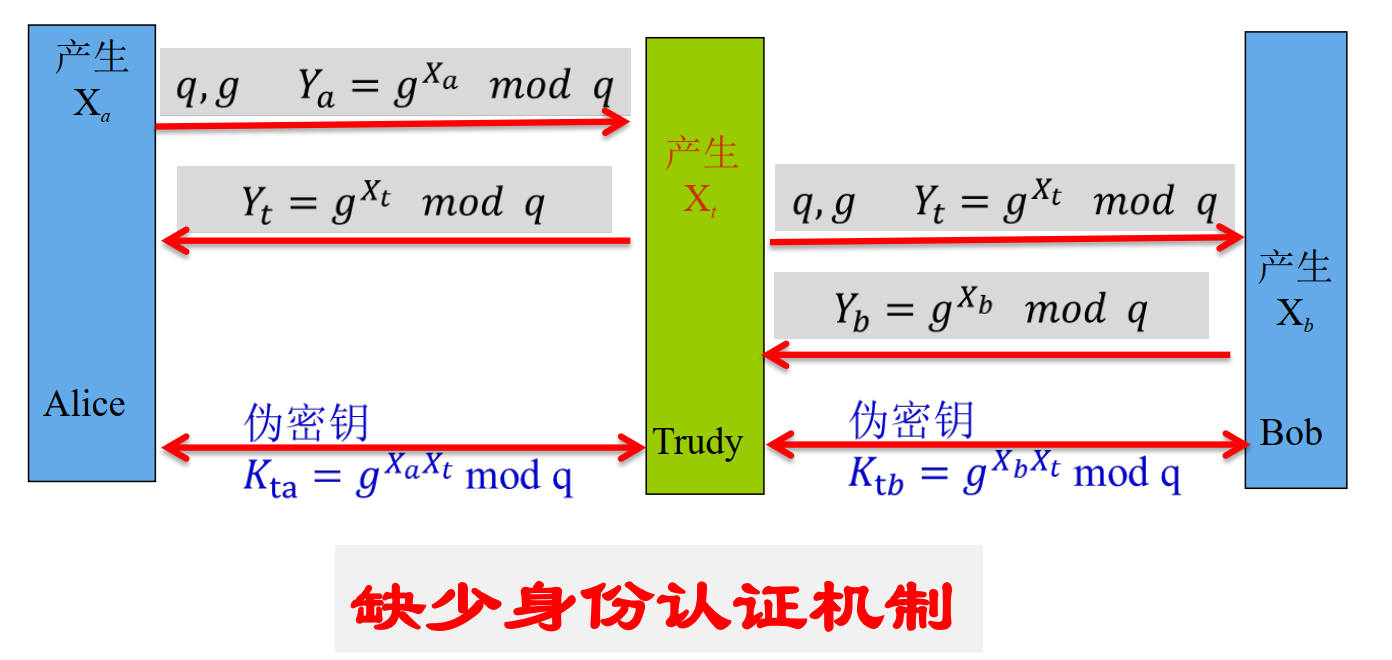
端-端密钥协商协议？
- 算法流程
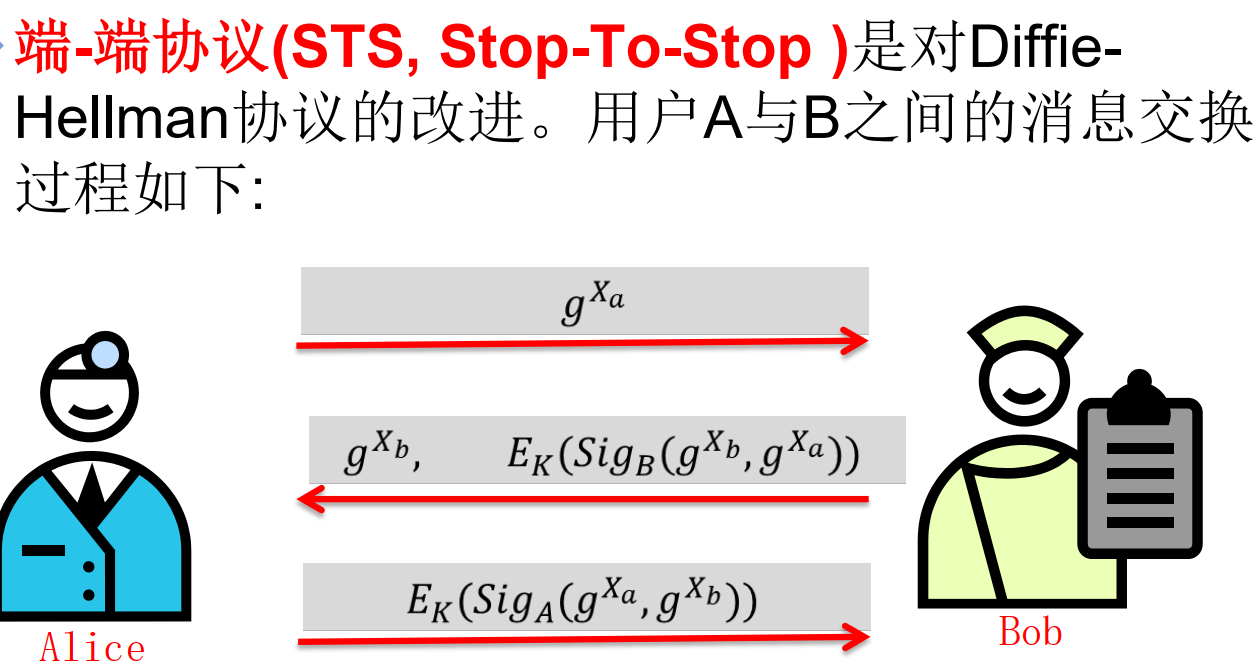
Shamir 秘密共享方案？
- 核心思想：
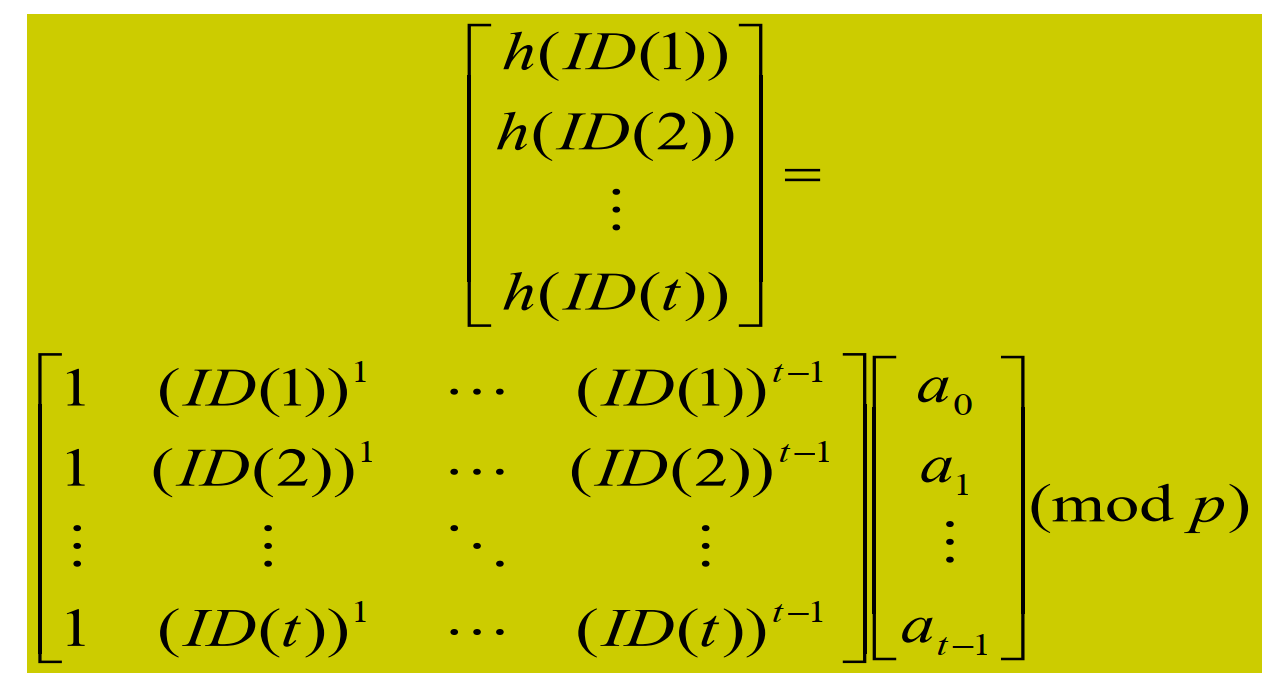
- 结论
  - 某t个参与者组合计算出的系数向量与另外t个参与者组合计算出的系数向量不相等时，这两次被组合的全部人员中必有“欺骗者”
  - 当某t个参与者组合计算出的系数向量与另外t个参与者组合计算出的系数向量相等时，（几乎可以断定）这两次被组合的全部人员都是诚实的参与者
零知识证明概念？